## Loading required package: ggplot2
## Loading required package: gridExtra
## Loading required package: reshape2
## Loading required package: VineCopula
## Loading required package: randtoolbox
## Loading required package: rngWELL
## This is randtoolbox. For an overview, type 'help("randtoolbox")'.
##
##
## This is version 1.2.0 of esgtoolkit. Starting with 1.0.0, package renamed as: 'esgtoolkit' (lowercase)
##
##
r0 <- 0.03
S0 <- 100
set.seed(10)
eps0 <- esgtoolkit::simshocks(n = 100, horizon = 3, frequency = "quart")
eps_trend <- eps0 + 0.1 * seq_len(nrow(eps0))
sim.GBM <- esgtoolkit::simdiff(n = 100, horizon = 3, frequency = "quart",
model = "GBM",
x0 = S0, theta1 = r0, theta2 = 0.1,
eps = eps0, seed=10001)
sim.GBM_trend <- esgtoolkit::simdiff(n = 100, horizon = 3, frequency = "quart",
model = "GBM",
x0 = S0, theta1 = r0, theta2 = 0.1,
eps = eps_trend, seed=10001)
(test1 <- esgtoolkit::esgmartingaletest(r = r0, X = sim.GBM, p0 = S0,
alpha = 0.05, method = "trend"))
## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo
## $model
##
## Call:
## lm(formula = Y ~ X_past - 1)
##
## Coefficients:
## X_past1 X_past2 X_past3 X_past4 X_past5 X_past6 X_past7 X_past8
## -0.06572 0.16730 -0.26443 -0.18877 0.19323 -0.02259 0.13619 -0.11573
## X_past9 X_past10 X_past11
## 0.03115 0.15059 -0.16763
##
##
## $confint
## 2.5 % 97.5 %
## X_past1 -1.5677993 1.43636442
## X_past2 -0.1809456 0.51555444
## X_past3 -0.5508806 0.02202036
## X_past4 -0.4761764 0.09862776
## X_past5 -0.1314138 0.51787217
## X_past6 -0.3278961 0.28271931
## X_past7 -0.1975848 0.46996836
## X_past8 -0.4314591 0.20000013
## X_past9 -0.2941281 0.35641929
## X_past10 -0.1642687 0.46545036
## X_past11 -0.4260530 0.09078976
##
## $regression_summary
##
## Call:
## lm(formula = Y ~ X_past - 1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12.9643 -3.4212 0.0955 2.9126 13.3615
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## X_past1 -0.06572 0.75596 -0.087 0.931
## X_past2 0.16730 0.17527 0.955 0.342
## X_past3 -0.26443 0.14416 -1.834 0.070 .
## X_past4 -0.18877 0.14464 -1.305 0.195
## X_past5 0.19323 0.16339 1.183 0.240
## X_past6 -0.02259 0.15365 -0.147 0.883
## X_past7 0.13619 0.16798 0.811 0.420
## X_past8 -0.11573 0.15890 -0.728 0.468
## X_past9 0.03115 0.16370 0.190 0.850
## X_past10 0.15059 0.15846 0.950 0.345
## X_past11 -0.16763 0.13006 -1.289 0.201
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.418 on 89 degrees of freedom
## Multiple R-squared: 0.118, Adjusted R-squared: 0.008978
## F-statistic: 1.082 on 11 and 89 DF, p-value: 0.3845
##
##
## $F_statistic
## value
## 1.082356
##
## $F_critical_value
## [1] 1.897906
##
## $F_p_value
## value
## 0.3845351
##
## $ADF_p_value
## [1] 0.99
##
## $Ljung_Box_p_value
## [1] 0.5478898
(test2 <- esgtoolkit::esgmartingaletest(r = r0, X = sim.GBM_trend, p0 = S0,
alpha = 0.05, method = "trend"))
## $model
##
## Call:
## lm(formula = Y ~ X_past - 1)
##
## Coefficients:
## X_past1 X_past2 X_past3 X_past4 X_past5 X_past6 X_past7
## -10.29737 0.24375 -0.37384 -0.28232 0.26141 -0.02530 0.19617
## X_past8 X_past9 X_past10 X_past11
## -0.15802 0.04407 0.17779 -0.12494
##
##
## $confint
## 2.5 % 97.5 %
## X_past1 -15.4669678 -5.12776227
## X_past2 -0.2665785 0.75408750
## X_past3 -0.7894330 0.04175475
## X_past4 -0.6930818 0.12845125
## X_past5 -0.1933910 0.71621916
## X_past6 -0.4424541 0.39186025
## X_past7 -0.2464075 0.63874666
## X_past8 -0.5622693 0.24622708
## X_past9 -0.3560678 0.44420838
## X_past10 -0.1924981 0.54806926
## X_past11 -0.4140250 0.16415292
##
## $regression_summary
##
## Call:
## lm(formula = Y ~ X_past - 1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -18.5358 -5.0704 0.1687 4.6036 20.1236
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## X_past1 -10.29737 2.60174 -3.958 0.000152 ***
## X_past2 0.24375 0.25684 0.949 0.345162
## X_past3 -0.37384 0.20916 -1.787 0.077286 .
## X_past4 -0.28232 0.20673 -1.366 0.175497
## X_past5 0.26141 0.22889 1.142 0.256484
## X_past6 -0.02530 0.20995 -0.120 0.904364
## X_past7 0.19617 0.22274 0.881 0.380844
## X_past8 -0.15802 0.20345 -0.777 0.439388
## X_past9 0.04407 0.20138 0.219 0.827275
## X_past10 0.17779 0.18636 0.954 0.342660
## X_past11 -0.12494 0.14549 -0.859 0.392804
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.979 on 89 degrees of freedom
## Multiple R-squared: 0.5878, Adjusted R-squared: 0.5368
## F-statistic: 11.54 on 11 and 89 DF, p-value: 4.801e-13
##
##
## $F_statistic
## value
## 11.53593
##
## $F_critical_value
## [1] 1.897906
##
## $F_p_value
## value
## 4.801344e-13
##
## $ADF_p_value
## [1] 0.99
##
## $Ljung_Box_p_value
## [1] 0.5813833
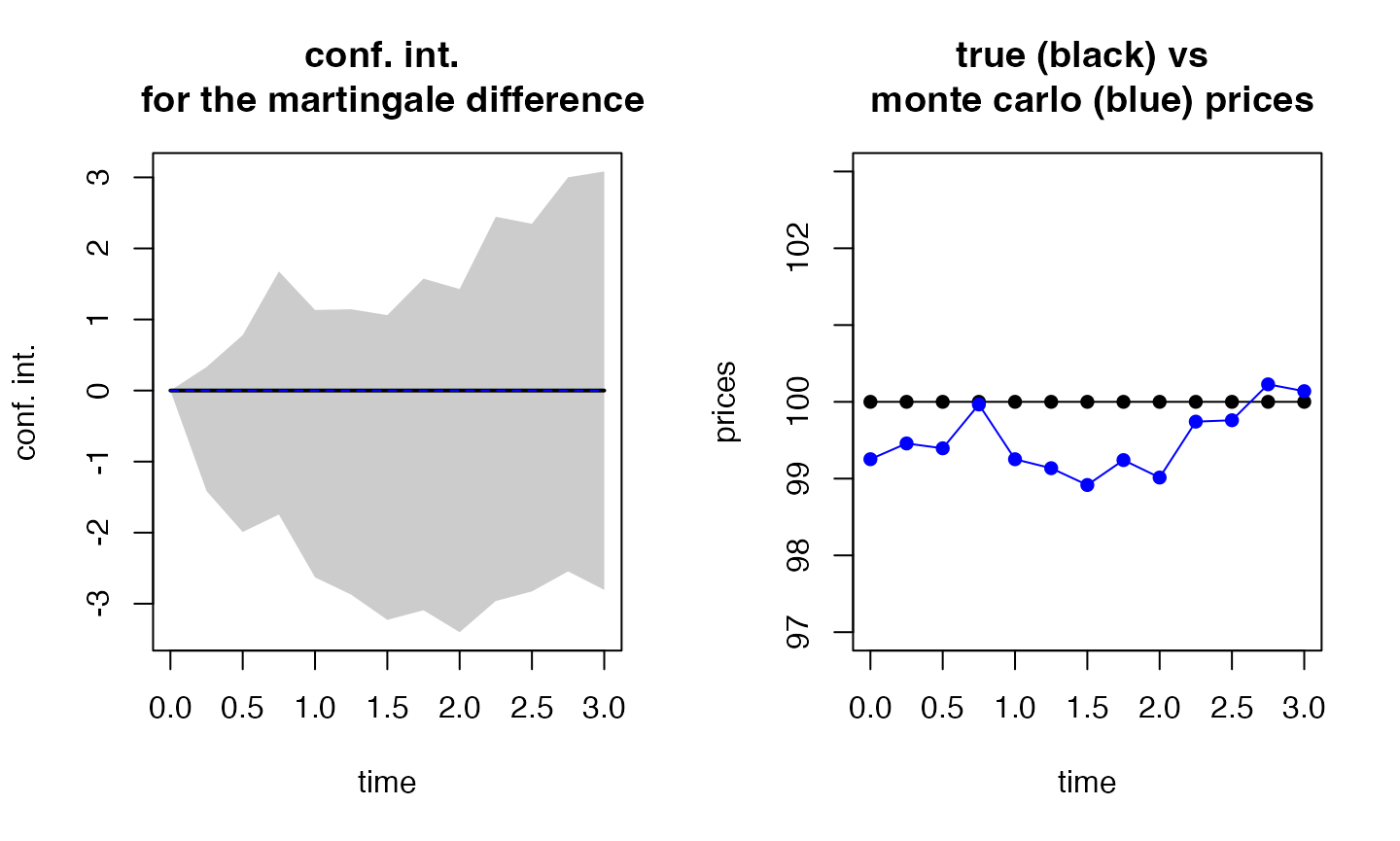
(test1_ratio <- esgtoolkit::esgmartingaletest(r = r0, X = sim.GBM, p0 = S0,
alpha = 0.05, method = "ratio"))
##
## One Sample t-test
##
## data: -log(Dt/Y)
## t = 3.6212, df = 1299, p-value = 0.0003045
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 0.004930759 0.016589169
## sample estimates:
## mean of x
## 0.01075996
(test2_ratio <- esgtoolkit::esgmartingaletest(r = r0, X = sim.GBM_trend, p0 = S0,
alpha = 0.05, method = "ratio"))
##
## One Sample t-test
##
## data: -log(Dt/Y)
## t = -28.306, df = 1299, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## -0.1381972 -0.1202828
## sample estimates:
## mean of x
## -0.12924
##
## martingale '1=1' one Sample t-test
##
## alternative hypothesis: true mean of the martingale difference is not equal to 0
##
## df = 99
## t p-value
## 0 Q2 -1.23133508 0.2211146
## 0 Q3 -0.86706246 0.3880045
## 0 Q4 -0.03979258 0.9683386
## 1 Q1 -0.78853728 0.4322667
## 1 Q2 -0.85421446 0.3950485
## 1 Q3 -1.00243504 0.3185774
## 1 Q4 -0.64526489 0.5202482
## 2 Q1 -0.81032744 0.4196956
## 2 Q2 -0.18944936 0.8501285
## 2 Q3 -0.18407588 0.8543305
## 2 Q4 0.16306302 0.8708012
## 3 Q1 0.09358936 0.9256245
##
## 95 percent confidence intervals for the mean :
## c.i lower bound c.i upper bound
## 0 Q1 0.000000 0.0000000
## 0 Q2 -1.415461 0.3314127
## 0 Q3 -1.990430 0.7798667
## 0 Q4 -1.744826 1.6762189
## 1 Q1 -2.629092 1.1337289
## 1 Q2 -2.872560 1.1435895
## 1 Q3 -3.227314 1.0608930
## 1 Q4 -3.092177 1.5745601
## 2 Q1 -3.400502 1.4284311
## 2 Q2 -2.961712 2.4454467
## 2 Q3 -2.826997 2.3470049
## 2 Q4 -2.545313 3.0011186
## 3 Q1 -2.804901 3.0825960
## $t
## Qtr1 Qtr2 Qtr3 Qtr4
## 0 -1.23133508 -0.86706246 -0.03979258
## 1 -0.78853728 -0.85421446 -1.00243504 -0.64526489
## 2 -0.81032744 -0.18944936 -0.18407588 0.16306302
## 3 0.09358936
##
## $p.value
## Qtr1 Qtr2 Qtr3 Qtr4
## 0 0.2211146 0.3880045 0.9683386
## 1 0.4322667 0.3950485 0.3185774 0.5202482
## 2 0.4196956 0.8501285 0.8543305 0.8708012
## 3 0.9256245
##
## $samplemean
## Qtr1 Qtr2 Qtr3 Qtr4
## 0 -0.54202403 -0.60528170 -0.03430376
## 1 -0.74768145 -0.86448540 -1.08321039 -0.75880860
## 2 -0.98603566 -0.25813277 -0.23999618 0.22790296
## 3 0.13884749
##
## $conf.int
## Series 1 Series 2
## 0 Q1 0.000000 0.0000000
## 0 Q2 -1.415461 0.3314127
## 0 Q3 -1.990430 0.7798667
## 0 Q4 -1.744826 1.6762189
## 1 Q1 -2.629092 1.1337289
## 1 Q2 -2.872560 1.1435895
## 1 Q3 -3.227314 1.0608930
## 1 Q4 -3.092177 1.5745601
## 2 Q1 -3.400502 1.4284311
## 2 Q2 -2.961712 2.4454467
## 2 Q3 -2.826997 2.3470049
## 2 Q4 -2.545313 3.0011186
## 3 Q1 -2.804901 3.0825960
##
## $truemean
## [1] 0 0 0 0 0 0 0 0 0 0 0 0 0
##
## $true_prices
## [1] 100 100 100 100 100 100 100 100 100 100 100 100 100
##
## $mc.prices
## [1] 99.25281 99.45798 99.39472 99.96570 99.25232 99.13551 98.91679
## [8] 99.24119 99.01396 99.74187 99.76000 100.22790 100.13885
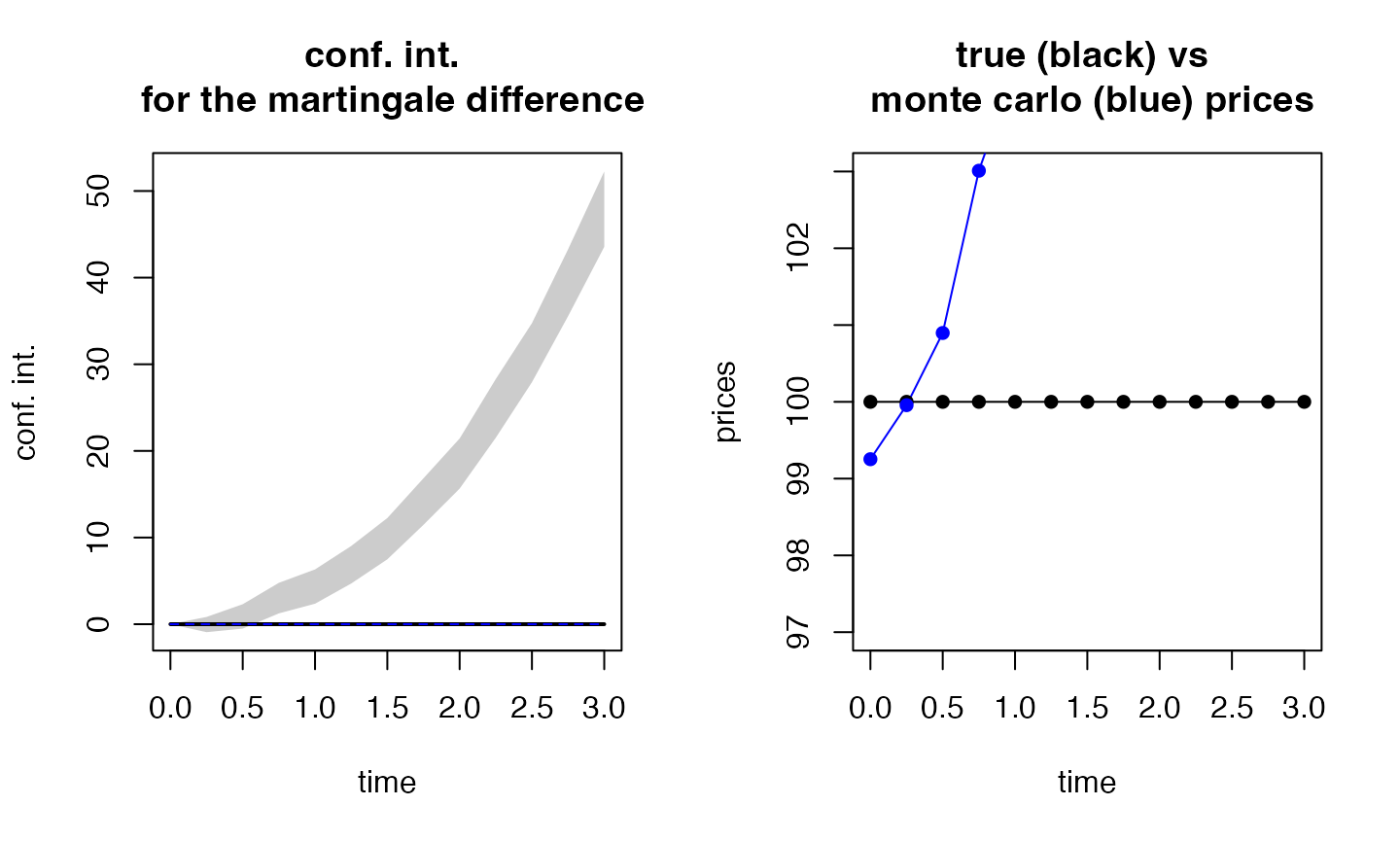
(test4 <- esgtoolkit::esgmartingaletest(r = r0, X = sim.GBM_trend, p0 = S0,
alpha = 0.05))
##
## martingale '1=1' one Sample t-test
##
## alternative hypothesis: true mean of the martingale difference is not equal to 0
##
## df = 99
## t p-value
## 0 Q2 -0.09830242 9.218909e-01
## 0 Q3 1.26564339 2.086113e-01
## 0 Q4 3.38854397 1.009793e-03
## 1 Q1 4.35501911 3.248801e-05
## 1 Q2 6.28558899 8.832209e-09
## 1 Q3 8.22182946 8.017342e-13
## 1 Q4 10.46406421 1.065632e-17
## 2 Q1 12.72722237 1.464574e-22
## 2 Q2 14.59789208 1.997160e-26
## 2 Q3 18.25662272 1.864629e-33
## 2 Q4 20.27387917 5.091006e-37
## 3 Q1 21.86138734 1.126498e-39
##
## 95 percent confidence intervals for the mean :
## c.i lower bound c.i upper bound
## 0 Q1 0.0000000 0.000000
## 0 Q2 -0.9213037 0.834326
## 0 Q3 -0.5092052 2.302959
## 0 Q4 1.2474891 4.772721
## 1 Q1 2.3632214 6.318966
## 1 Q2 4.6921279 9.021072
## 1 Q3 7.4864493 12.249406
## 1 Q4 11.4705294 16.838555
## 2 Q1 15.6505958 21.431879
## 2 Q2 21.5232520 28.294760
## 2 Q3 27.9312389 34.742971
## 2 Q4 35.5563641 43.271273
## 3 Q1 43.5552945 52.251014
## $t
## Qtr1 Qtr2 Qtr3 Qtr4
## 0 -0.09830242 1.26564339 3.38854397
## 1 4.35501911 6.28558899 8.22182946 10.46406421
## 2 12.72722237 14.59789208 18.25662272 20.27387917
## 3 21.86138734
##
## $p.value
## Qtr1 Qtr2 Qtr3 Qtr4
## 0 9.218909e-01 2.086113e-01 1.009793e-03
## 1 3.248801e-05 8.832209e-09 8.017342e-13 1.065632e-17
## 2 1.464574e-22 1.997160e-26 1.864629e-33 5.091006e-37
## 3 1.126498e-39
##
## $samplemean
## Qtr1 Qtr2 Qtr3 Qtr4
## 0 -0.04348885 0.89687710 3.01010493
## 1 4.34109374 6.85659997 9.86792776 14.15454224
## 2 18.54123730 24.90900609 31.33710516 39.41381860
## 3 47.90315446
##
## $conf.int
## Series 1 Series 2
## 0 Q1 0.0000000 0.000000
## 0 Q2 -0.9213037 0.834326
## 0 Q3 -0.5092052 2.302959
## 0 Q4 1.2474891 4.772721
## 1 Q1 2.3632214 6.318966
## 1 Q2 4.6921279 9.021072
## 1 Q3 7.4864493 12.249406
## 1 Q4 11.4705294 16.838555
## 2 Q1 15.6505958 21.431879
## 2 Q2 21.5232520 28.294760
## 2 Q3 27.9312389 34.742971
## 2 Q4 35.5563641 43.271273
## 3 Q1 43.5552945 52.251014
##
## $truemean
## [1] 0 0 0 0 0 0 0 0 0 0 0 0 0
##
## $true_prices
## [1] 100 100 100 100 100 100 100 100 100 100 100 100 100
##
## $mc.prices
## [1] 99.25281 99.95651 100.89688 103.01010 104.34109 106.85660 109.86793
## [8] 114.15454 118.54124 124.90901 131.33711 139.41382 147.90315